Ex_09.cpp File Reference

Finds eigenvalues for streamwise-constant linearized Navier-Stokes equations, in two ways: More...

Detailed Description

Finds eigenvalues for streamwise-constant linearized Navier-Stokes equations, in two ways:

1. By solving for the generalized eigenvalue problem:

   \[ \left[ \begin{array}{cc} \Delta & 0\\ 0 & I \end{array} \right]\partial_t \left[ \begin{array}{c} v\\ \eta \end{array} \right]\;=\;\left[ \begin{array}{cc} \frac{1}{Re}\Delta^2 & 0\\ -i\,k_z\,U' & \frac{1}{Re}\Delta \end{array} \right]\left[ \begin{array}{c} v \\ \eta \end{array} \right] \]

   with boundary conditions \(v(\pm 1) \;=\; v'(\pm 1) \;=\; \eta(\pm 1) \;=\; 0\)
2. By solving the generalized eigenvalue problem:

   \[ \left[ \begin{array}{cccc} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 0 \\ \end{array} \right]\partial_t \left[ \begin{array}{c} u \\ v \\ w \\ p \end{array} \right] \;= \; \left[ \begin{array}{cccc} \frac{1}{Re}\Delta & -U' & 0 & 0 \\ 0 & \frac{1}{Re}\Delta & 0 & -\partial_y \\ 0 & 0 & \frac{1}{Re}\Delta & -ik_z \\ 0 & \partial_y & ik_z & 0 \\ \end{array} \right]\left[ \begin{array}{c} u \\ v \\ w \\ p \end{array} \right] \]

   with boundary conditions \(u(\pm 1,t) \;=\; v(\pm 1,t) \;=\; w(\pm 1,t) \;=\; [\mathrm Dv(\cdot,t)](\pm 1) \;=\; 0\)

Note from the above form that the eigenvalues are simply the eigenvalues of \( \Delta^2/Re\) and \(\Delta/Re\), both of whom are real. Method 2 approximates the solution more accrately than method 1, as imaginary parts in method 2 are zero to machine precision. Here, \( \mathrm D = \mathrm d/\mathrm d y \).

Definition in file Ex_09.cpp.

Include dependency graph for Ex_09.cpp:

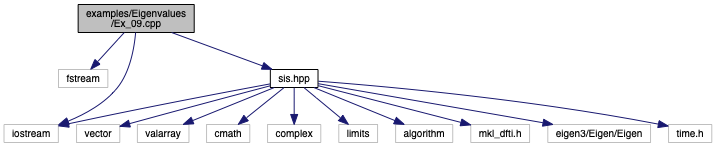
Go to the source code of this file.

Macros
#define	SIS_USE_LAPACK

Functions
int	main ()

Macro Definition Documentation

SIS_USE_LAPACK

#define SIS_USE_LAPACK

Definition at line 70 of file Ex_09.cpp.

Function Documentation

main()

int main

(

)

Definition at line 77 of file Ex_09.cpp.

References sis::Linop< T >::coef, sis::GeneralizedEigenSolver< T >::compute(), sis::GeneralizedEigenSolver< T >::eigenvalues, sis::BcMat< T >::eval, ii(), ind, sis::BcMat< T >::L, sis::N, sis::Linop< T >::n, std::pow(), sis::LinopMat< T >::resize(), sis::BcMat< T >::resize(), sis::Linop< T >::set(), sis::setChebPts(), sis::sis_setup(), and sis::y().